Struct tinyraytracer::vectors::Vec3

pub struct Vec3 {
    x: f32,
    y: f32,
    z: f32,
}

3-D vector, this struct includes functions for conveniently perform

Fields

x: f32

y: f32

z: f32

Implementations

impl Vec3

pub fn orig() -> Self

Create an origin vector (0, 0, 0)

pub fn new(v: (f32, f32, f32)) -> Self

Create a new vector by specifying its coordinates

pub fn l2(&self) -> f32

Get the L2 norm of the vector. L_2 norm is the length of the vector, in 3-D space is basically the distance of a vector from the origin. Let say you have 2 vectors v1 and v2, running (v1-v2).l2() will give you the distance between those points. That is, the distance between v_1 and v_2 is the length of a vector from v_1 to v_2

pub fn dot(&self, other: &Self) -> f32

This gives us the Dot Product of 2 vectors. This is a very useful quantity for projection of vectors. Key property of the dot-product is this: What this means is that the dot-product of two vectors is a product of their lengths and the cosine of the angle between them. Vector Projection

pub fn cross(&self, other: &Self) -> Self

Cross Product

This gives us a vector that is orthogonal to self and other with norm of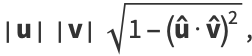

pub fn project_on(&self, other: &Self) -> Self

Helper function that finds the projection of a vector to another vector. I’m going to expand on this at some point. If you don’t understand what’s going on in this function I strongly recommend this series of videos 3Brown1Blue’s Essence of Linear Algebra

pub fn normalized(&self) -> Self

Get 1-norm vector

pub fn mult(&self, v: f32) -> Self

Multiply a vector by a scalar

pub fn reflect(&self, normal: Vec3) -> Self

Find a reflection of a vector, from a surface generated by a normal.

pub fn refract(&self, normal: Vec3, refract_index: f32) -> Self

Trait Implementations

impl Add<Vec3> for Vec3

type Output = Vec3

The resulting type after applying the + operator.

fn add(self, other: Self) -> Vec3

Performs the + operation.

impl Clone for Vec3

fn clone(&self) -> Vec3

Returns a copy of the value.

pub fn clone_from(&mut self, source: &Self)

Performs copy-assignment from source.

impl Debug for Vec3

fn fmt(&self, f: &mut Formatter<'_>) -> Result

Formats the value using the given formatter.

impl Sub<Vec3> for Vec3

type Output = Vec3

The resulting type after applying the - operator.

fn sub(self, other: Self) -> Vec3

Performs the - operation.

impl Copy for Vec3